Cargando...
Números naturales
Son los que toman intervalos discretos de una unidad, y empiezan con el número 1, extendiéndose hasta el infinito. Una forma de distinguir estos números es como aquellos que sirven para contar. Notación: N = {1, 2, 2, 4, 5,...} = {N \ 0}
Números enteros
Este conjunto incluye al conjunto de los números naturales, al cero y a aquellos números que también toman intervalos discretos, pero que tienen un signo negativo por delante. Notación: Z = {-∞, ..., -4, -3, -2, -1, 0, 1, 2, 3, 4,...,∞ }
Por ejemplo, el opuesto de 10 es -10.
Números racionales
Este conjunto incluye a los enteros y a todos aquellos que pueden expresarse como el cociente de dos números enteros, de manera que pueden tener una parte decimal.
Notación: Q
Q= {-∞,.-1000,…- 15/2,…-7,…-8/3,…0,…1,...,- 81/4,…,∞}
Números irracionales
A este conjunto pertenecen los números que no pueden expresarse como el cociente de dos números enteros, tampoco se puede especificar una parte periódica que se repita, aunque la cantidad de sus cifras decimales se extiendan hasta al infinito.
Notación: Q´
Ejemplos de números irracionales:
Raíces inexactas:

Los conjuntos de números irracionales y racionales son disjuntos. Es decir, no tienen ningún elemento en común.
Números reales
El conjunto de los números reales incluye tanto a los números racionales como a los irracionales. Es decir, los números reales van desde el menos infinito hasta el más infinito. R= (-∞,∞)
Números imaginarios

Números complejos
Son números que tienen una parte real y una parte imaginaria. Forma; a + b i (a y b son números reales). Importante: en el conjunto de números complejos podemos observar números reales puros e imaginarios puros.
Notación: C
Ejemplos: 2 + 5 i; 7 - 4i ; - 2 - 3 i; 8i ; 9
Para comprender mejor, observemos el diagrama de Venn que representa en formagráfica a los conjuntos definidos anteriormente.
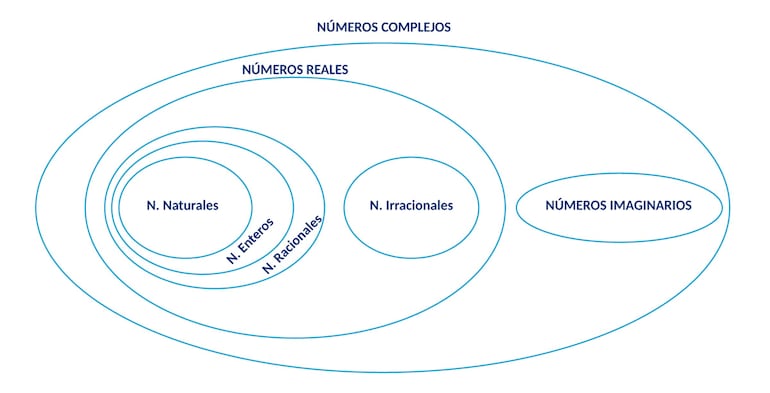
Destaquemos que algunos números pertenecen a varios conjuntos, para ello damos algunos ejemplos.
El número 2 es natural, entero, racional, real y complejo. El -3 es entero, racional, real y complejo. El 2/5 es racional, real y complejo. El √8 es irracional, real y complejo. El -8 es imaginario y complejo.


