Cargando...
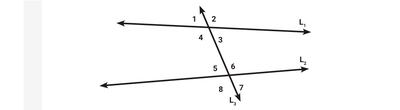
Estudiaremos los ángulos que se forman cuando una recta (L3), llamada transversal, corta a otras dos rectas (L1 y L2).
Ángulos alternos internos: son los que están en la franja que se forma entre las dos rectas L1 y L2 y en lados opuestos de la transversal L3. En nuestro ejemplo son el par 4 y 6 y el par de ángulos 3 y 5.
Ángulos alternos externos: son los que están fuera de la franja que se forma entre las dos rectas L1 y L2 y en lados opuestos de la transversal L3. En nuestro ejemplo son el par 1 y 7 y el par de ángulos 2 y 8.
Ángulos correspondientes: son los que están en posiciones similares con respecto a la transversal, uno con respecto a la recta L1 y el otro con respecto a la recta L2. En nuestro ejemplo son el par 1 y 5, el par de ángulos 2 y 6, el par 4 y 8 y el par de ángulos 3 y 7.
Ángulos conjugados: son los ángulos que están o dentro o fuera de la franja entre las rectas L1 y L2 y del mismo lado de la transversal L3. Pueden ser conjugados internos, si están dentro de la franja y en nuestro ejemplo son los pares 4 y 5 y los pares 3 y 6 y conjugados externos, si están fuera de la franja, y en nuestro ejemplo son los pares 1 y 8 y los pares 2 y 7.
Si las rectas L1 y L2 son paralelas se cumplen ciertas relaciones entre los ángulos.
Lea más: Ángulos. Definición. Cómo se nombran. Clasificación
Aprende más
Resuelve los siguientes ejercicios aplicando las propiedades estudiadas de los ángulos.
